isukerantaro
Lớp trưởng


Tổng số bài gửi : 57
Join date : 09/08/2010
Age : 29
Đến từ : 10T1
 |  Tiêu đề: Tổng kết các dạng của Bất Đẳng Thức Cauchy (ôn tập KT 1 tiết) Tiêu đề: Tổng kết các dạng của Bất Đẳng Thức Cauchy (ôn tập KT 1 tiết)  12/2/2011, 23:35 12/2/2011, 23:35 | |
| Dựa theo chương trình học trên lớp và các bài tập đã làm, Linh xin rút ra một số dạng A-G (Cauchy) thường dùng để CM bất đẳng thức
Cái này là kinh nghiệm làm bài của cá nhân, nên khi viết sẽ khá khó hiểu, nên bạn nào có thắc mắc gì cứ post bài hỏi nhé. Bái viết chỉ có tác dụng đúc kết các dạng đã học, không phải bài giảng, nên chỉ viết ngắn gọn thôi, nếu phần nào chưa rõ, các bạn nên tham khảo thêm các sách và các ví dụ của thầy cô trên lớp
1. Tích/ tổng không đổi
- Phương pháp: Cộng/nhân thêm số
VD1:
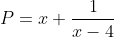
Phân tích và giải:
Thêm 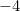 với mục đích cho tích của 2 số =const với mục đích cho tích của 2 số =const
VD2:
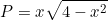
Phân tích và giải
Để ý khi  và và 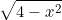 bình phương thì 2 đại lượng sẽ có tổng không đổi => dùng cauchy cho 2 số này bình phương thì 2 đại lượng sẽ có tổng không đổi => dùng cauchy cho 2 số này
2. Tách từ ẩn
- Phương pháp: Thường với bài toán này cho ở dạng tổng, có phân số => ta tách ẩn x từ đề bài sao cho khi nhân vào có tổng không đổi (thật ra cách này cũng tương tự dạng 1, tuy nhiên với ẩn)
VD1:
=x+\frac{1}{{x}^{2}})
Phân tích và giải
ta thấy ở mẫu có 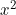 mà trên có x => nghĩ đến việc tìm thêm 1 x nữa => tách mà trên có x => nghĩ đến việc tìm thêm 1 x nữa => tách 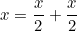 khi dùng Cauchy sẽ mất hết x khi dùng Cauchy sẽ mất hết x
3. Điểm rơi của Cauchy
- Phương pháp:
1. Dự đoán dấu “=”
2. Tách các số hạng của đầu bài ra (chú ý đến chiều BĐT)
3. Áp dụng BĐT Cauchy và giả thiết đề bài CM BĐT
VD: Tìm min
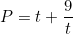 với với 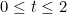
Phân tích và giải
Dấu bằng khi t=2
Ta tách như sau
Để ý chiều BĐT là 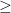 mà mà 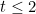 nên ta sẽ tách nên ta sẽ tách 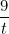 (mục đích là t ở mẫu ta sẽ được chiều (mục đích là t ở mẫu ta sẽ được chiều 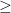 ) )
Mặt khác t = 2
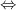 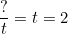 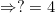
Từ đó ta tách như sau:
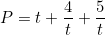 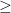 ... ...
4. Dạng phân số 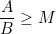
- Phương pháp: Dùng BĐT Cauchy cho 2 số: 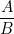 và và 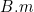
1. Dự đoán dấu “=”
2. Tìm ra m (khi 2 đại lượng bằng nhau) (nhớ chú ý chọn m phù hợp): Các bạn xem kĩ phần này trong tài liệu, có cần thì mình cung cấp cho
3. Thêm bớt lượng 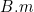
4. Dùng Cauchy cho 2 đại lượng đó rồi cộng từng vế
5. Đánh giá đại lượng cần thêm bớt (Nếu cần)
Các bạn thứ giải VD sau theo pp trên:
CM:
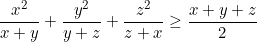
5. BĐT hoán vị vòng quanh (a,b,c bình đẳng)
- Phương pháp: Do vài trò a, b,c bình đẳng nên chỉ cần xét 1 đại lượng (cách này lớp mình luyện nhiều nên nói sơ vậy thôi)
6. Tìm quan hệ giữa giả thiết và biểu thức cần cm
- Phương pháp: Cộng thêm, hoặc biến đổi đưa về đại lượng đầu bài\
VD:
Cho 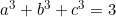
Chứng minh: 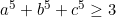
(Xem bài giải trong tập)
Next: Tổng hợp các dạng của BĐT Buinhiacôpsky
Cảm ơn các bạn đã đọc bài viết. Mong bài viết này có thể giúp các bạn đúc kết tốt hơn các dạng để thuận lợi hơn trong việc ôn tập. Mong các bạn ôn tập thật tốt cho kì KT sắp tới.
Bài viết hay thì thanks hộ nhé     | |
|









